Abstract
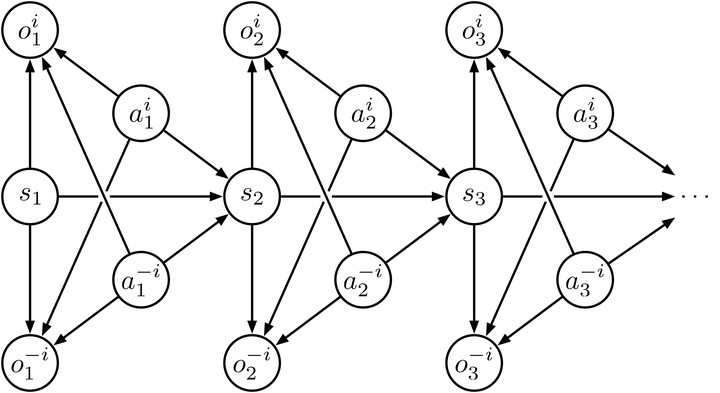
In a single-agent setting, reinforcement learning (RL) tasks can be cast into an inference problem by introducing a binary random variable o, which stands for the ‘optimality’. In this paper, we redefine the binary random variable o in multi-agent setting and formalize multi-agent reinforcement learning (MARL) as probabilistic inference. We derive a variational lower bound of the likelihood of achieving the optimality and name it as Regularized Opponent Model with Maximum Entropy Objective (ROMMEO). From ROMMEO, we present a novel perspective on opponent modeling and show how it can improve the performance of training agents theoretically and empirically in cooperative games. To optimize ROMMEO, we first introduce a tabular Q-iteration method ROMMEO-Q with proof of convergence. We extend the exact algorithm to complex environments by proposing an approximate version, ROMMEO-AC. We evaluate these two algorithms on the challenging iterated matrix game and differential game respectively and show that they can outperform strong MARL baselines.
Ying Wen
Assistant Professor
My research interests include multi-agent learning and reinforcement learning..